Disaster by Design/ Safety by Intent #40
Disaster by Design
Jorge Agustin Nicolás Ruiz de Santayana y Borrás, also known as George Santayana, wrote that “Those who cannot remember the past are condemned to repeat it.” Disaster by Design/Safety by Intent #39 described the partial meltdown of the reactor core at the Sodium Reactor Experiment (SRE) in California. Workers at the Fermi Unit 1 reactor in Michigan must have remembered this accident pretty well, since they duplicated almost every key aspect of it just seven years later.
So, perhaps a companion to Santayana’s point is “Those who remember the past are condemned to repeat it, unless they take steps to prevent it.” Had SRE’s owners copyrighted their accident script, Fermi Unit 1’s owner would probably have had to mail them a royalty check.
Fermi Unit 1(Newport, MI) – October 1966
Unit 1 at the Enrico Fermi Atomic Power Plant had a fast breeder reactor cooled by liquid sodium. The operators achieved initial criticality of the reactor on August 23, 1963. An extensive testing program kept the reactor at very low power levels—too low to make electricity—until December 29, 1965. Completion of the low-power testing program enabled the operators to increase the reactor power level to the 10% and later 50% power testing plateaus.
The 50% testing plateau included a 60-hour steady state run that began on August 5, 1966, and ended on August 7. During this run, workers noticed abnormally high temperatures of the liquid sodium flowing out of some fuel elements. Outlet temperatures 20 to 25% higher for one fuel element than outlet temperatures for other fuel elements had been observed during June 1966. The outlet temperatures were 40 to 47% above other outlet temperatures during the August 1966 run at 50% power.
The reactor was shut down after the 60-hour run. Workers relocated four fuel elements that exhibited high outlet temperatures to other positions in the reactor core. They wanted to determine whether the high temperatures were caused by the fuel elements or were due to faulty thermocouples providing falsely high indications.
The operators restarted the reactor on October 4, 1966. They slowly and steadily increased the reactor power level. By the mid-afternoon of October 5, the reactor power level had reached about 15%. Plant parameters did not look right to the operators. The outlet temperatures of some fuel elements still indicated abnormally high. And now the operators noticed that the control rods were more withdrawn from the reactor core than expected for this power level.
At 3:09 pm, plant conditions deteriorated further. The radiation monitors in the ventilation exhaust ducts from the reactor building alarmed and automatically shut dampers to isolate flow to the environment from this pathway. This radiation monitor’s reading could not be easily dismissed as a faulty instrument—radiation monitors in four other areas of the plant were also indicating high readings. The operators shut down the reactor.
Debris in the reactor
Two fuel elements were found to have partially melted due to inadequate cooling. A crumpled piece of metal was recovered from the core sodium inlet plenum at the bottom of the reactor vessel below the reactor core region. Media reports at the time claimed that a beer can left inside the vessel or piping during construction blocked flow through the reactor core and caused the partial meltdown.
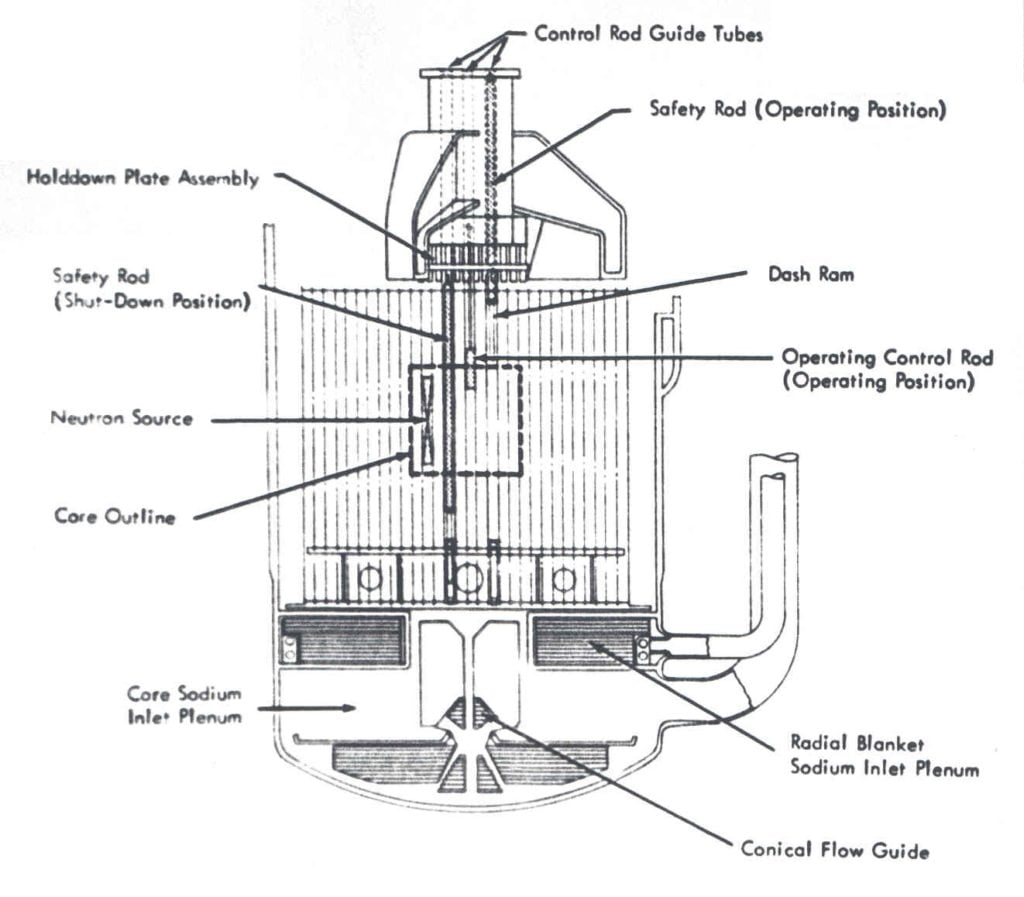
Fig. 1 (Source: U.S. Department of Energy)
Examination of the metal debris determined that neither alcohol nor poor housekeeping caused the partial meltdown. Instead, a feature installed late in the reactor’s design intended to provide better protection in event of a meltdown triggered a meltdown.
The primary system consisted of three piping loops. Each loop supplied liquid sodium to the bottom of the reactor vessel. Vertical metal panels helped re-direct the horizontal flow from the loops upward to flow vertically through the reactor core. Warmed passing through the reactor core, the loops routed the liquid sodium to heat exchangers to convert the thermal energy into electricity.
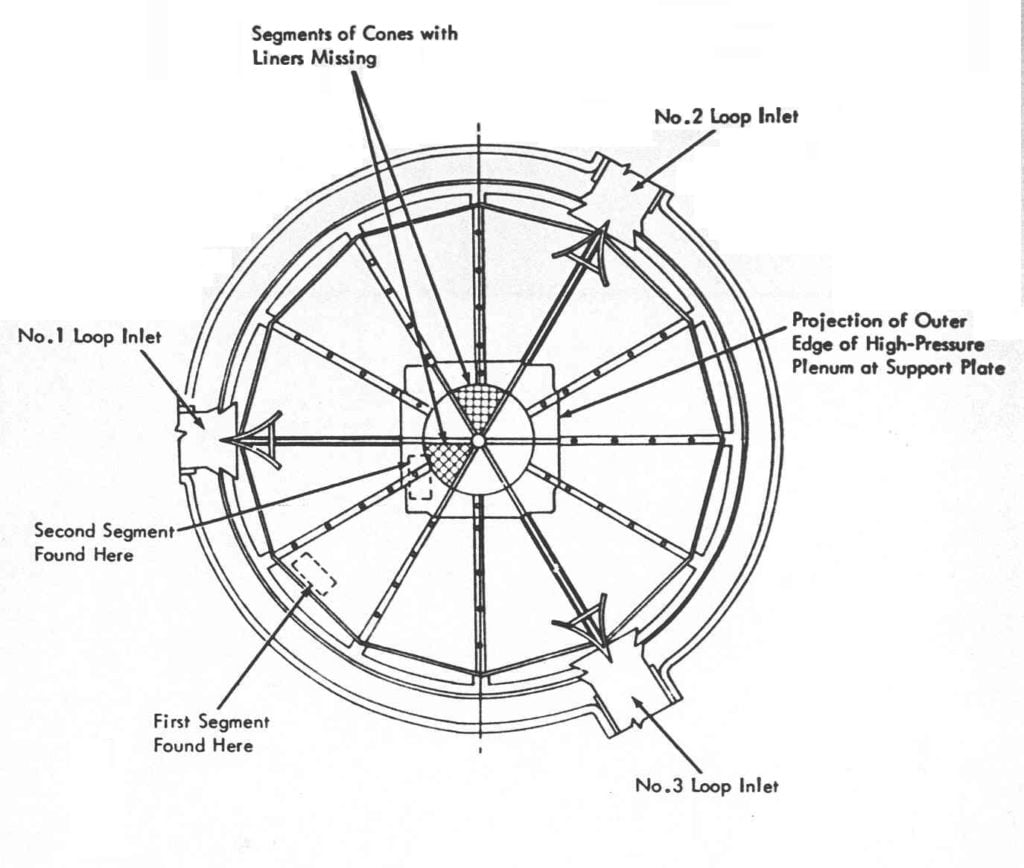
Fig. 2 (Source: U.S. Department of Energy)
As the plant’s design neared completion, someone posited that the lava-like molten material from a reactor core meltdown would be funneled down onto the vertical metal panels. The concern was that concentrating the molten material could allow formation of a critical mass of the uranium and plutonium. In other words, the nuclear chain reaction could inadvertently restart at the bottom of the reactor vessel.
The solution to this postulated problem was to install conical flow guides. These flow guides were pie-shaped pieces of metal. Their wide ends (the crust ends) were welded to the bottom of the core sodium inlet plenum. Their narrow ends (the pointy ends of the pie pieces) were welded to the corners formed by the vertical metal panels. These flow guides would assist re-directing the incoming liquid sodium up through the reactor core. In event of a core meltdown, the flow guides would spread out the molten material dropping down from above, lessening the chances of forming a critical mass.
A thin liner made of zirconium metal was applied to the upper surfaces of the six conical flow guides. Zirconium is a metal with a high melting point; the metal rods containing the fuel pellets are made from a zirconium alloy. The zirconium liners protected the conical flow guides from the high temperature of molten material.
Two of the six zirconium liners came loose from their conical flow guides and were carried upward by the liquid sodium flow. The flow stuck them to the bottom of the reactor core where they obstructed cooling flow through some of the fuel elements causing two to overheat and partially melt.
Workers removed the two damaged fuel elements, inspected the remainder for signs of damage, and tidied up the primary system. Workers also removed the conical flow guides after determining they lacked a useful safety function. The reactor restarted years later.
Missed Opportunities = Pre-Existing Problems = Reactor Accident
Like the sinking of the Titanic leading to the capsizing of the Eastland three years later, the good intention of making the plant safer actually compromised its safety.
During the review of the proposed design change to install the conical flow guides, asking and answering the question of “what if” the liner breaks loose could have avoided this meltdown. The conical flow guides were removed from Fermi before the reactor restarted, strongly suggesting they were never needed in the first place. Had a compelling case been made to install the flow guides, the design review process could have foreseen the liner’s failure and evolved to a more robust configuration for the flow guides.
During operation in June 1966, thermocouples indicated abnormally high temperatures of the liquid sodium flowing out of some fuel elements. Such warnings are precisely why the thermocouples were installed; they were not installed to free up shelf space out at the warehouse. But workers dismissed the alarming indications as potentially being caused by faulty thermocouples.
So, workers moved fuel elements around inside the reactor core in an attempt to check whether the thermocouples were providing valid indications. They restarted the reactor. Lo and behold, the abnormally high temperatures were still present.
Control rods had to be withdrawn farther than expected. Afterwards, the reason was attributed to part of the reactor core melting and no longer being in place to sustain the nuclear chain reaction. With part of the reactor core missing in action, the control rods had to be withdrawn farther to expose more of the reactor core in compensation. At the time, workers did not understand the reason for the control rod positioning—they merely noted it and proceeded to further damage the reactor core.
They continued operating the reactor with several indications of inadequate core cooling until the inadequately cooled reactor released radiation that set off all kinds of radiation alarms.
Safety by Intent
Disaster by Design/Safety by Intent #39 described how workers at SRE failed to recognize numerous warning signs that inadequate cooling was damaging the reactor core. That commentary also conceded that hindsight is nearly always 20/20.
Whatever excuses the SRE workers had for failing to connect the dots and see a meltdown in progress, the workers at Fermi Unit 1 had fewer excuses. They could have, and should have, benefitted from the meltdown at SRE to recognize sooner that they were replicating it almost step by step. Instead, they repeated every step and reached the same destination.
Both reactors had indications of high temperatures from some fuel locations. Workers at both reactors attributed the indications to faulty instruments. Reality revealed the instruments to be true and the attributions to be faulty.
Both reactors experienced control rods being withdrawn farther than expected. Workers at both reactors did not know why. Reality revealed the melting reactor cores removed fuel from the nuclear engines, requiring the gas pedals to be depressed farther.
Both reactors had design flaws that caused inadequate cooling of the reactor core. Workers at both reactors modified the plants to remedy the design flaws, but too late to prevent the meltdowns.
While no sodium-cooled reactors currently operate in the United States, the U.S. Department of Energy (DOE) is working with industry on a number of “advanced” reactor designs, including the Sodium-Cooled Fast Reactor (SFR). One of the SFR’s safety advantages, to quote the DOE, is that the design provides a “Long grace period for corrective action, if needed.” SRE’s meltdown transpired over a two-week period. Fermi Unit 1 had indications of inadequate core cooling in June that were repeated in August and dismissed until extensive damage occurred in October 1966. The “if needed” grace period is never long enough when warning sign after warning sign is dismissed or ignored.
DOE did acknowledge some “challenges” for the SFR: their higher speed and higher energy neutrons can embrittle and degrade nearby materials, liquid sodium coolant reactors with air and water and degrades concrete, and the opaqueness of the liquid sodium coolant complicates in-service inspections and maintenance.
Thank goodness for the “Long grace period for corrective actions, if needed.” That and the fact that SFRs only operate in cyberspace where the primary threat is carpal tunnel syndrome.
—–
UCS’s Disaster by Design/Safety by Intent series of blog posts is intended to help readers understand how a seemingly unrelated assortment of minor problems can coalesce to cause disaster and how effective defense-in-depth can lessen both the number of pre-existing problems and the chances they team up.
