As North Korea continues its missile development, a key question is what it may have learned from its recent missile test that is relevant to building a reentry vehicle (RV) for a long-range missile.
The RV is a crucial part of a ballistic missile. A long-range missile accelerates its warhead to very high speed—16,000 mph—and sends it arcing through space high above the atmosphere. To reach the ground it must reenter the atmosphere. Atmospheric drag slows the RV and most of the kinetic energy it loses goes into heating the air around the RV, which then leads to intense heating of the surface of the RV. The RV absorbs some of the heat, which is conducted inside to where the warhead is sitting.
So the RV needs to be built to (1) withstand the intense heating at its outer surface, and (2) insulate the warhead from the absorbed heat that is conducted through the interior of the RV.
The first of these depends on the maximum heating rate at the surface and the length of time that significant heating takes place. Number (2) depends on the total amount of heat absorbed by the RV and the amount of time the heat has to travel from the surface of the RV to the warhead, which is roughly the time between when intense heating begins and when the warhead detonates.
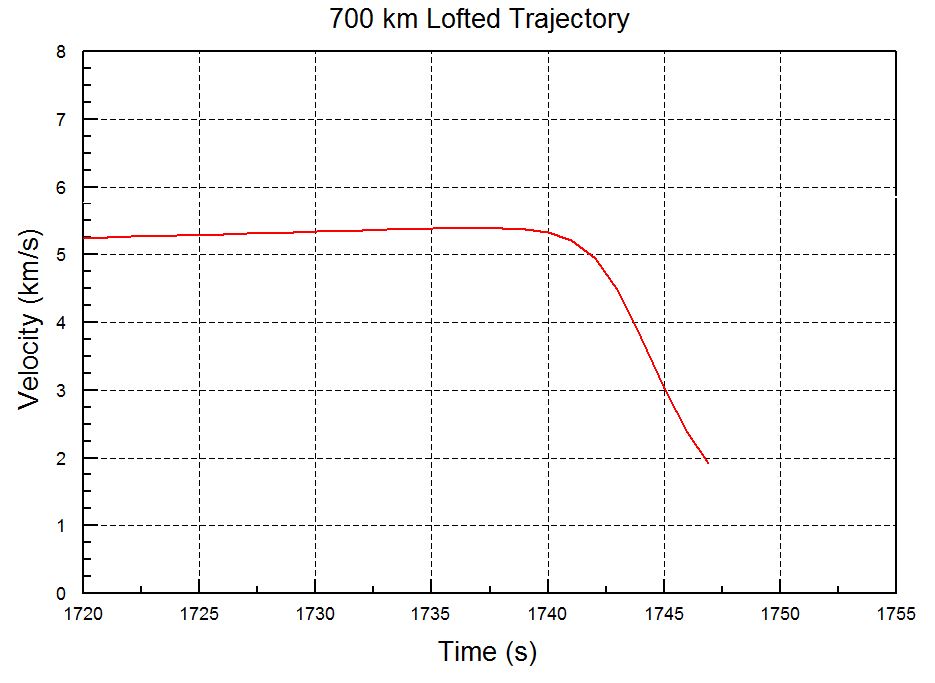
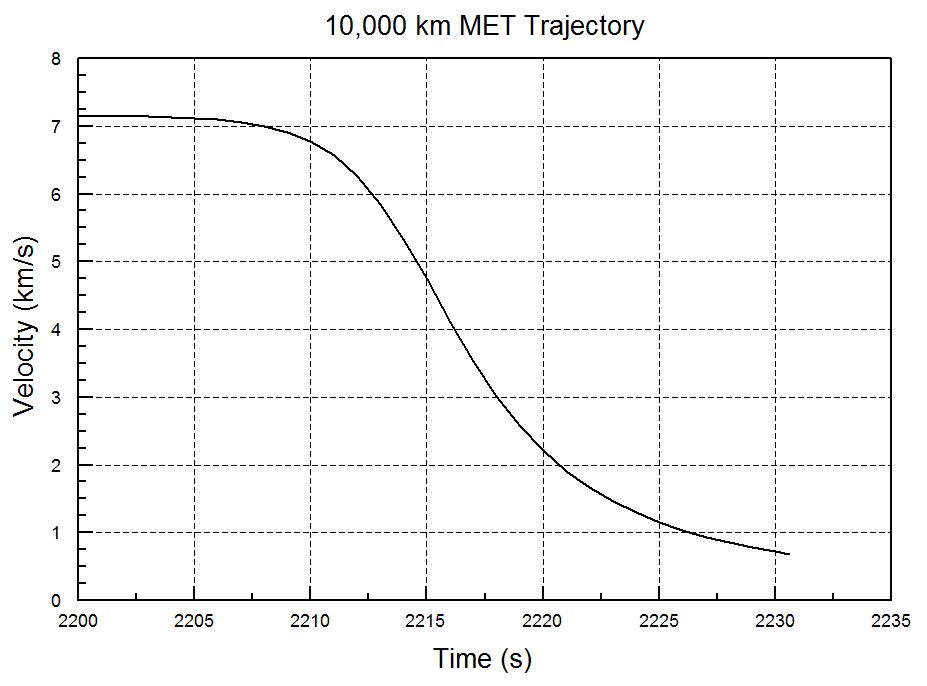
I calculated these quantities for the two cases of interest here: the highly lofted trajectory that the recent North Korean missile followed and a 10,000 km missile on a normal (MET) trajectory. The table shows the results.
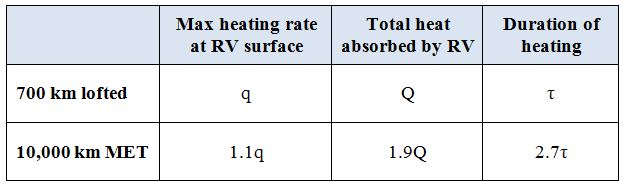
The maximum heating rate (q) is only about 10% higher for the 10,000 km range missile than the lofted missile. However, the total heat absorbed (Q) is nearly twice as large for the long-range missile and the duration of heating (τ) is more than two and a half times as long.
This shows that North Korea could get significant data from the recent test—assuming the RV was carrying appropriate sensors and sent that information back during flight, and/or that North Korea was able to recover the RV from the sea. But it also shows that this test does not give all the data you would like to have to understand how effective the heatshield might be before putting a nuclear warhead inside the RV and launching it on a long-range missile.
Some details
The rate of heat transfer per area (q) is roughly proportional to ρV3, where ρ is the atmospheric density and V is the velocity of the RV. Since longer range missiles reenter at higher speeds, the heating rate increases rapidly with missile range. The total heat absorbed (Q) is the integral of q over time during reentry.
This calculation assumes the ballistic coefficient (β) of the RV is 48 kN/m2 (1,000 lb/ft2). The heating values in the table roughly scale with β. A large value of β means less atmospheric drag so the RV travels through the atmosphere at higher speed. That increases the accuracy of the missile but also increases the heating. The United States worked for many years to develop RVs with special coatings that allowed them to have high β and therefore high accuracy, but could also withstand the heating under these conditions.
The results in the table can be understood by looking at how RVs on these two trajectories slow down as they reenter. Figs. 1 and 2 plot the speed of the RV versus time; the x and y axes of the two figures have the same scale. The maximum deceleration (slope of the curve) is roughly the same in the two cases, leading to roughly the same value of q. But the 10,000 km range missile loses more total energy—leading to a larger value of Q—and does so over a longer time than the lofted trajectory.